Currently, when we test multi-thread Java we call the class under test by as many threads possible. And since the test is not deterministic, we repeat this test as often as possible.

This approach has the disadvantage that most of the time our faulty test succeeds which makes debugging multi-threaded bugs a nightmare. I, therefore, developed an open-source tool, vmlens, to make JUnit test of multi-threaded Java deterministic. And to make debugging easier.

The idea is to execute all possible thread interleavings for a given test. And to report the failed thread interleaving which makes debugging possible.

A test for a concurrent counter

The following example shows how to use vmlens to write a test for a concurrent counter. All tests are in the GitHub project vmlens-examples in the package com.vmlens.examples.tutorial.counter.

import com.vmlens.api.AllInterleavings;
public class TestCounterNonVolatile {
 int i = 0;
 @Test
 public void test() throws InterruptedException {
   try (AllInterleavings allInterleavings = 
     new AllInterleavings
        ("tutorial.counter.TestCounterNonVolatile");) {
	 while (allInterleavings.hasNext()) {
	  i = 0;
	  Thread first = new Thread(() -> {
		i++;
	  });
	  Thread second = new Thread(() -> {
		i++;
	  });
	  first.start();
	  second.start();

	  first.join();
	  second.join();
				
	  assertEquals(2,i);
     }
   }
 }
}

We increment the field i from two threads. And after both threads are finished we check that the count is 2. The trick is to surround the complete test by a while loop iterating over all thread interleavings using the class AllInterleavings.

vmlens uses byte code transformation to calculate all thread interleavings. Therefore you need to configure vmlens in the maven pom as described here. After running the test, we can see the result of all test runs in the interleave report in the file target/interleave/elements.html.

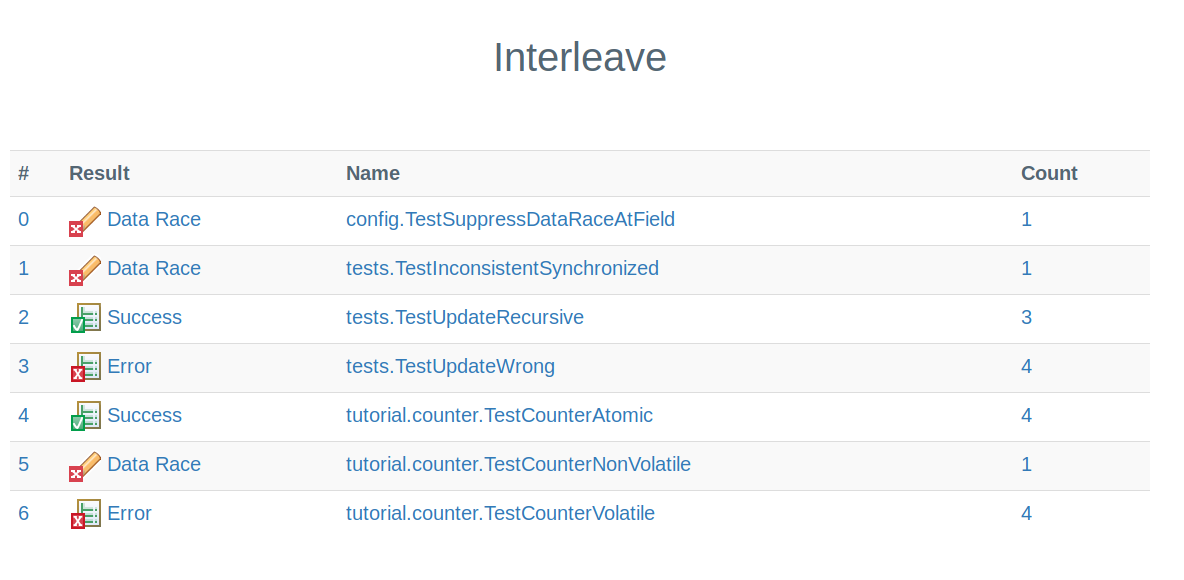
Our test, test number 5 with the name tutorial.counter.TestCounterVolatile, failed with a data race. A data race means that the reads and writes to a shared field are not correctly synchronized. Incorrectly synchronized reads and writes can be reordered by the JIT compiler or the CPU. Here can is important. Typically incorrectly synchronized reads and writes return the correct result. Only under very specific circumstances, often a combination of a specific CPU architecture, a specific JVM, and a specific thread interleaving, lead to incorrect values.

vmlens checks for every field access if it is correctly synchronized to detect data races.

A test for a concurrent volatile counter

To fix the data race we declare the field as volatile:

public class TestCounterVolatile {
 volatile int i = 0;
 @Test
 public void test() throws InterruptedException {
   try (AllInterleavings allInterleavings = 
	  new AllInterleavings
	    ("tutorial.counter.TestCounterVolatile");) {
	  while (allInterleavings.hasNext()) {
	   i = 0;
	   Thread first = new Thread(() -> {
		 i++;
	   });
	   Thread second = new Thread(() -> {
		 i++;
	   });
	   first.start();
	   second.start();

	   first.join();
	   second.join();
				
	   assertEquals(2,i);
	  }
   }
 }
}

This fixes the data race but now the assertion fails:

TestCounterVolatile.test:30 expected:<2> but was:<1>

To see what went wrong we click on the test tutorial.counter.TestCounterVolatile in the interleave report. This shows us the interleaving which went wrong:

The bug is that both threads first read the variable i and after that, both update the variable. So the second thread overrides the value of the first one.

A test witch an atomic counter

To write a correct concurrent counter we use the class AtomicInteger:

public class TestCounterAtomic {
 AtomicInteger i = new AtomicInteger();
 @Test
 public void test() throws InterruptedException {
   try (AllInterleavings allInterleavings = 
	  new AllInterleavings
         ("tutorial.counter.TestCounterAtomic");) {
	  while (allInterleavings.hasNext()) {
	   i.set(0);
	   Thread first = new Thread(() -> {
		i.incrementAndGet();
	   });
	   Thread second = new Thread(() -> {
	    i.incrementAndGet();
	   });
	   first.start();
	   second.start();

	   first.join();
	   second.join();
	   assertEquals(2,i.get());
	  }
   }
  }
}

Now the increment of our counter is atomic and our test finally succeeds.

Conclusion

As we have seen executing all thread interleavings for multi-threaded tests make multi-threaded tests deterministic. And it makes debugging of failed tests possible. To test all thread interleavings we have surrounded our test by a while loop iterating over all thread interleavings using the class AllInterleavings. vmlens uses byte code transformation to calculate all thread interleavings. Therefore you also need to configure vmlens in the maven pom as described here. And if a test fails you can look at the failing thread interleaving to debug our test.